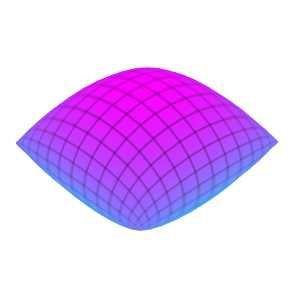
Template: Graphics/3d-parametric-chart
Discription: This template creates a parametric Bouligand cushion surface with a set of parametric equations.
Link: Click this link to see the live chart or shape.
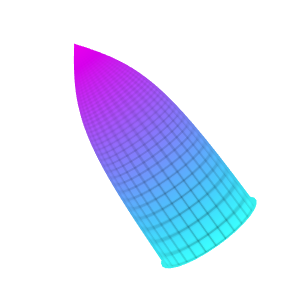
Template: Graphics/3d-parametric-chart
Discription: This template creates a parametric bullet nose surface with a set of parametric equations.
Link: Click this link to see the live chart or shape.
Template: Graphics/3d-parametric-chart
Discription: The circled helicoid can be generated by the helical movement of a circle. This surface is created by extending a sphere along a diameter and then twisting.
Link: Click this link to see the live chart or shape.

Template: Graphics/3d-parametric-chart
Discription: This template creates a 3D surface with a set of parametric cosine-sine equations
Link: Click this link to see the live chart or shape.
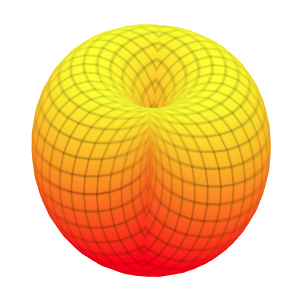
Template: Graphics/3d-parametric-chart
Discription: Cross-gap is a representation of the projective plane. It is like a shrinked torus where there is no middle hole and the side has been pinched together in such a way that the top cross to the bottom.
Link: Click this link to see the live chart or shape.

Template: Graphics/3d-parametric-chart
Discription: Dini surface is a surface with constant negative curvature that can be created by twisting a pseudosphere. It is named after Ulisse Dini.
Link: Click this link to see the live chart or shape.
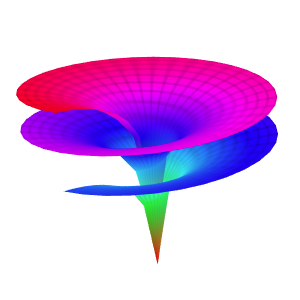
Template: Graphics/3d-parametric-chart
Discription: This template creates a drop surface with a set of parametric equations.
Link: Click this link to see the live chart or shape.
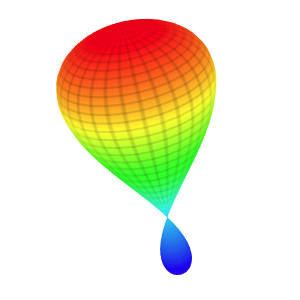
Template: Graphics/3d-parametric-chart
Discription: An elliptic cone is a type of quadric surfaces. A quadric surface is a generalization of conic sections (ellipses, parabolas, and hyperbolas).
Link: Click this link to see the live chart or shape.
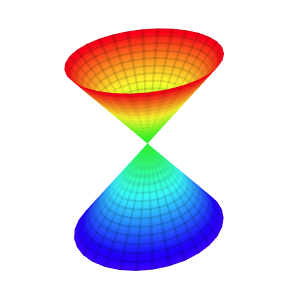
Template: Graphics/3d-parametric-chart
Discription: Elliptic cyclide is a type of Dupin cyclides. Dupin cyclide is any geometric inversion of a standard torus, cylinder, or double cone. Dupin cyclides are natural objects in Lie sphere geometry.
Link: Click this link to see the live chart or shape.
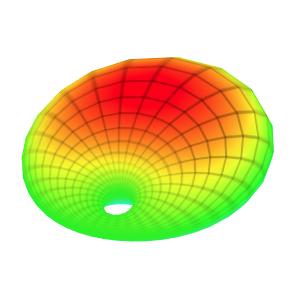
Template: Graphics/3d-parametric-chart
Discription: The Globoid surface can be generated by rotation of an arc of the circle about the z-axis lying at the plane of the arc.
Link: Click this link to see the live chart or shape.
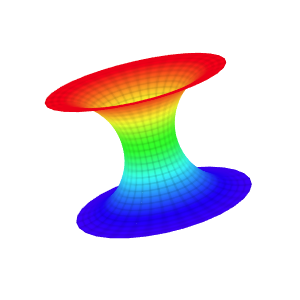
Template: Graphics/3d-parametric-chart
Discription: A helicoid is a trace of a line. For any point on the surface, there is a line on the surface passing through it. Helicoids are shaped like screws and can be described be a set of parametric equations.
Link: Click this link to see the live chart or shape.
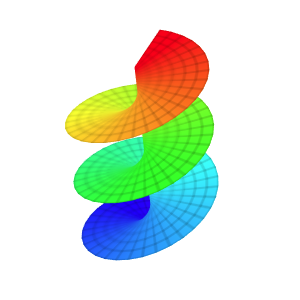
Template: Graphics/3d-parametric-chart
Discription: In geometry, a hyperboloid is a type of quadric surfaces. A quadric surface is a generalization of conic sections (ellipses, parabolas, and hyperbolas).
Link: Click this link to see the live chart or shape.
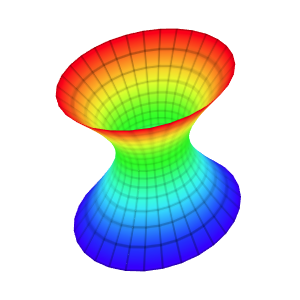
Template: Graphics/3d-parametric-chart
Discription: A Klein bottle is an example of a non-orientable surface. It is a 2D manifold against which a system for determining a normal vector cannot be consistently defined. It is a one-side surface that, if traveled upon, could be followed back to the point of origin while flipping the traveler upside down.
Link: Click this link to see the live chart or shape.
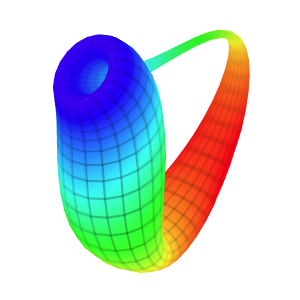
Template: Graphics/3d-parametric-chart
Discription: The Moebius strip is a surface with only one side. It has the mathematical property of being unorientable. It can be realized as a ruled surface. It has Euler characteristic of 0.
Link: Click this link to see the live chart or shape.
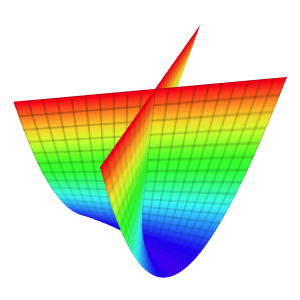
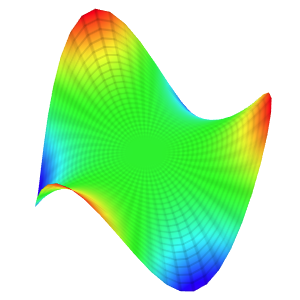
Template: Graphics/3d-parametric-chart
Discription: The monkey saddle surface belongs to the class of saddle surfaces and its name derives from the observation that a saddle for a monkey requires three depressions: two for the legs, and one for the tail.
Link: Click this link to see the live chart or shape.
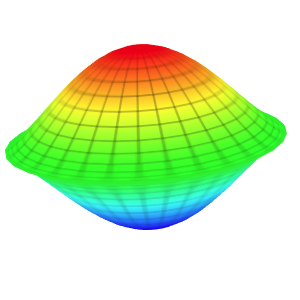
Template: Graphics/3d-parametric-chart
Discription: This template creates a parametric soucoupoid surface with a set of parametric equations.
Link: Click this link to see the live chart or shape.
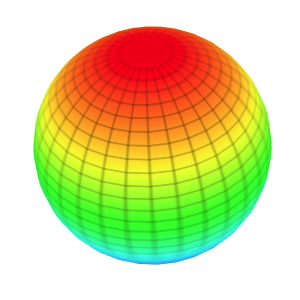
Template: Graphics/3d-parametric-chart
Discription: This template creates a parametric sphere surface with a set of parametric equations.
Link: Click this link to see the live chart or shape.
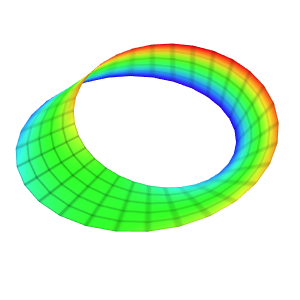
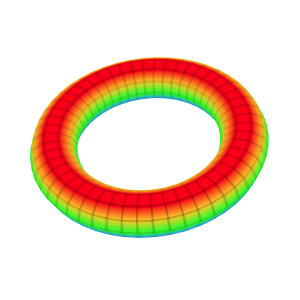
Template: Graphics/3d-parametric-chart
Discription: A torus is a surface of revolution generated by revolving a circle in 3D space about an axis coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus.
Link: Click this link to see the live chart or shape.
Template: Graphics/3d-parametric-chart
Discription: A Whitney umbrella is a self-intersecting surface placed in 3D space. It is the union of all straight lines that pass through points of a fixed parabola and are perpendicular to a fixed straight line, parallel to the axis of the parabola and lying on its perpendicular bisecting plane.
Link: Click this link to see the live chart or shape.