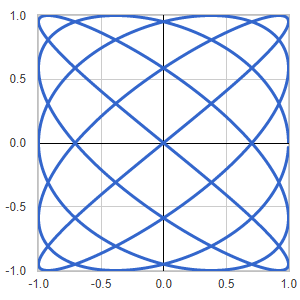
Template: Graphics/2d-parametric-chart
Discription: In mathematics, a Lissajous curve is a graph of a system of parametric equations that describe complex harmonic motion. The appearance of the curve is highly sensitive to the ratio of a/b .
Link: Click this link to see the live chart or shape.
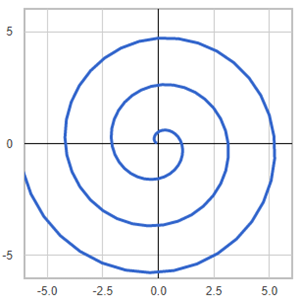
Template: Graphics/2d-parametric-chart
Discription: The Archemedean spiral is a spiral named after Greek mathematician Archimedes. It is the locus of points corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line rotates with constant angular velocity.
Link: Click this link to see the live chart or shape.
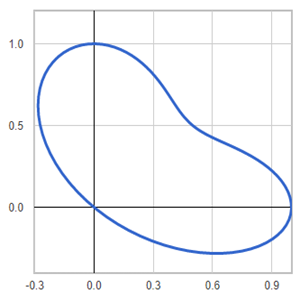
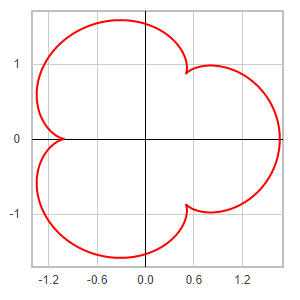
Template: Graphics/2d-parametric-chart
Discription: Bean shape created using 2D parametric equations.
Link: Click this link to see the live chart or shape.
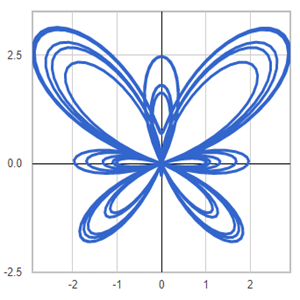
Template: Graphics/2d-parametric-chart
Discription: Butterfly shape created using 2D parametric equations.
Link: Click this link to see the live chart or shape.
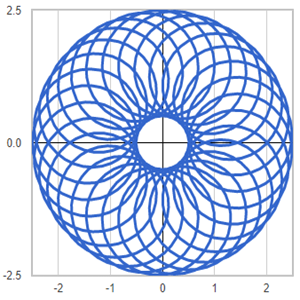
Template: Graphics/2d-parametric-chart
Discription: Circles created using 2D parametric equations.
Link: Click this link to see the live chart or shape.
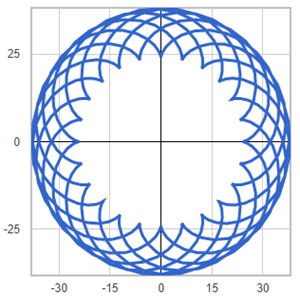
Template: Graphics/2d-parametric-chart
Discription: Circular shape created using 2D parametric equations.
Link: Click this link to see the live chart or shape.
Template: Graphics/2d-parametric-chart
Discription: Cycloid is the trace of a point on a circle rolling upon another circle without slipping. When a circle is rolling externally upon a fixed circle - in the same manner a coin rolls around another - we have epicycloid. When the rolling is internal, we have hypocycloid.
Link: Click this link to see the live chart or shape.
Template: Graphics/2d-parametric-chart
Discription: Cycloid is the trace of a point on a circle rolling upon another circle without slipping. When a circle is rolling externally upon a fixed circle - in the same manner a coin rolls around another - we have epicycloid. When the rolling is internal, we have hypocycloid.
Link: Click this link to see the live chart or shape.
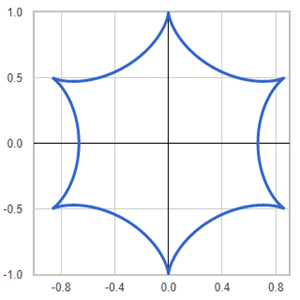
Template: Graphics/2d-parametric-chart
Discription: Cycloid is the trace of a point on a circle rolling upon another circle without slipping. When a circle is rolling externally upon a fixed circle - in the same manner a coin rolls around another - we have epicycloid. When the rolling is internal, we have hypocycloid.
Link: Click this link to see the live chart or shape.
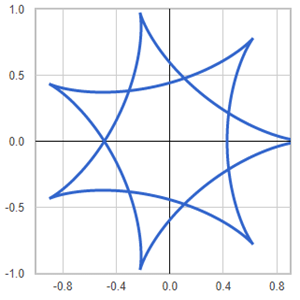
Template: Graphics/2d-parametric-chart
Discription: Cycloid is the trace of a point on a circle rolling upon another circle without slipping. When a circle is rolling externally upon a fixed circle - in the same manner a coin rolls around another - we have epicycloid. When the rolling is internal, we have hypocycloid.
Link: Click this link to see the live chart or shape.
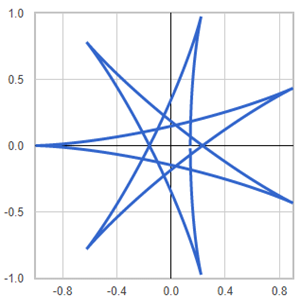
Template: Graphics/2d-parametric-chart
Discription: Cycloid is the trace of a point on a circle rolling upon another circle without slipping. When a circle is rolling externally upon a fixed circle - in the same manner a coin rolls around another - we have epicycloid. When the rolling is internal, we have hypocycloid.
Link: Click this link to see the live chart or shape.
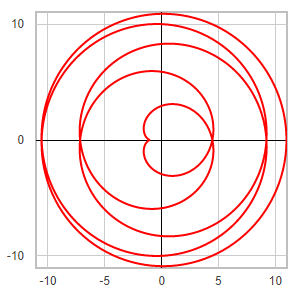
Template: Graphics/2d-parametric-chart
Discription: Cycloid is the trace of a point on a circle rolling upon another circle without slipping. When a circle is rolling externally upon a fixed circle - in the same manner a coin rolls around another - we have epicycloid. When the rolling is internal, we have hypocycloid.
Link: Click this link to see the live chart or shape.
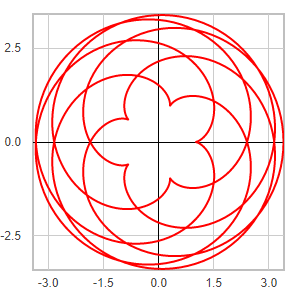
Template: Graphics/2d-parametric-chart
Discription: Cycloid is the trace of a point on a circle rolling upon another circle without slipping. When a circle is rolling externally upon a fixed circle - in the same manner a coin rolls around another - we have epicycloid. When the rolling is internal, we have hypocycloid.
Link: Click this link to see the live chart or shape.
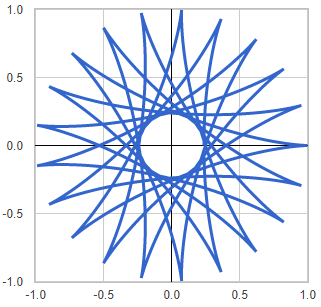
Template: Graphics/2d-parametric-chart
Discription: Flower shape created using 2D parametric equations.
Link: Click this link to see the live chart or shape.
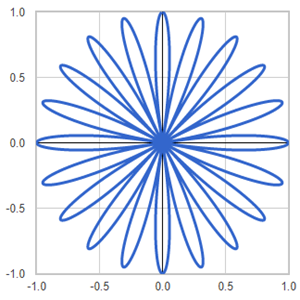
Template: Graphics/2d-parametric-chart
Discription: Lattice shape created using 2D parametric equations.
Link: Click this link to see the live chart or shape.
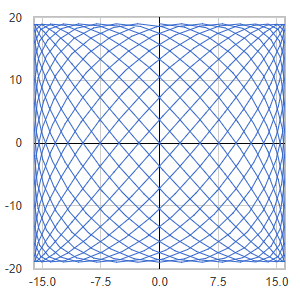
Template: Graphics/2d-parametric-chart
Discription: Lattice shape created using 2D parametric equations.
Link: Click this link to see the live chart or shape.
Template: Graphics/2d-parametric-chart
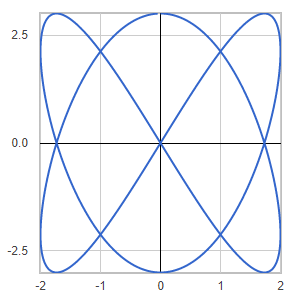
Discription: Lattice shape created using 2D parametric equations.
Link: Click this link to see the live chart or shape.
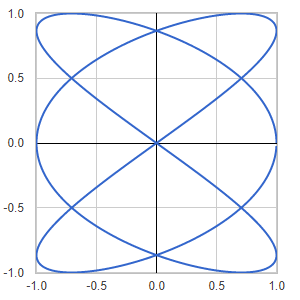
Template: Graphics/2d-parametric-chart
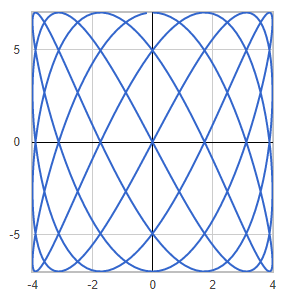
Discription: In mathematics, a Lissajous curve is a graph of a system of parametric equations that describe complex harmonic motion. The appearance of the curve is highly sensitive to the ratio of a/b .
Link: Click this link to see the live chart or shape.